by Piero Massimino
by Piero MassiminoOsservatorio Astrofisico
Astrophysical Observatory
Catania - Italy
 by Piero Massimino
by Piero Massimino
Osservatorio Astrofisico
Astrophysical Observatory
Catania - Italy
Meridiana Solare Verticale
Caratteristica di ogni tipo di meridiana solare è quella di poter indicare il Tempo Vero Locale; possiamo considerarla un orologio che come lancetta utilizza proprio ed esclusivamente il Sole e, come tacca oraria, lo stilo della meridiana, per cui ogni qualvolta (una volta al giorno) l’estremità dell’ombra dello stilo viene a contatto con la medesima linea tracciata sulla meridiana, la Terra avrà compiuto, rispetto al Sole, esattamente una rotazione attorno al proprio asse. Vi sarà spesso però una certa approssimazione, rispetto all’orario indicato dal nostro orologio da polso (anche se il luogo in cui ci troviamo è situato proprio sul meridiano che stabilisce il fuso orario, nel caso dell’Italia il TMEC), dovuta sia al fatto che la Terra, nel compiere la rivoluzione attorno al Sole, non mantiene costante la sua velocità, essendo la sua orbita ellittica, e sia perché l’inclinazione dell’asse di rotazione della Terra rispetto al piano della sua orbita (67.56 gradi), rende sinusoidale il movimento apparente del Sole sulla volta celeste, per cui alle volte l’estremità dell’ombra dello stilo toccherà in anticipo la relativa linea oraria, altre volte in ritardo.
Quella particolare linea tracciata nei pressi della linea oraria delle 12, chiamata analemna, e che, indifferentemente, potrebbe essere tracciata vicino a qualunque linea oraria, viene calcolata tenendo in considerazione l’E.T. (Equazione del Tempo), cioè quel ritardare o anticipare dovuto al non uniforme moto della Terra attorno al Sole: essa permette di avere piena corrispondenza tra l’ora indicata dalla meridiana ed il Tempo Medio Locale.
Costruire una meridiana solare verticale di per sé non è complicato, ed anche i calcoli da fare per poter correttamente tracciare ogni linea componente la meridiana stessa non implicano complesse conoscenze astronomiche se non trigonometriche: basta applicare correttamente le formule basilari. Da qui ad istruire, o meglio, programmare un computer per evitare lunghi e tediosi calcoli il passo è breve: tutti i personal computer, così diffusi ai giorni nostri, possono benissimo soddisfare tali esigenze. Conoscendo uno qualunque dei tanti linguaggi di programmazione è quindi possibile generare il software opportuno che non solo permetterà di effettuare i calcoli ma anche di rappresentare graficamente i risultati così ottenuti.
Il personal computer
non calcola una sola cosa, che resta quindi di esclusiva pertinenza umana:
l’inclinazione della parete su cui si vuole costruire la meridiana solare. Quando il
suddetto muro non è orientato perfettamente verso sud, si dice che è declinante di un
angolo inferiore a zero se declina verso ovest-nord-ovest (ovest-sud-ovest per
l’emisfero meridionale), maggiore a zero se verso est-nord-est (est-sud-est per
l’emisfero meridionale). Ovviamente tale angolo sarà uguale a zero se il muro è
posto esattamente a sud. Per conoscere tale angolo basta piantare, su una tavola di legno,
un chiodo di una decina di centimetri di lunghezza, facendo in modo che la punta sporga di
una lunghezza determinabile, e poggiare tale supporto sulla parete in questione (Fig.1).
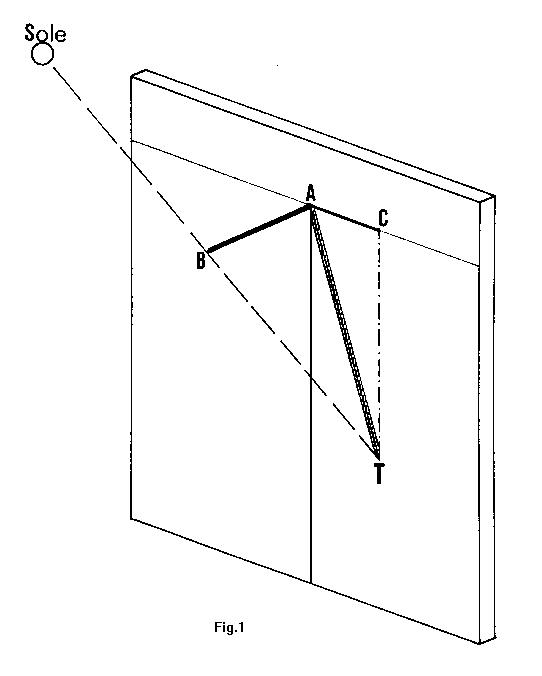
Adesso non ci resta che aspettare il momento in cui il Sole, passando al nostro meridiano, proietti l’ombra del chiodo sulla tavola. Per stabilire il momento esatto possiamo fare senz’altro riferimento al nostro orologio da polso, avendo avuto prima l’accortezza di esserci informati circa la longitudine del luogo su cui ci troviamo ed avere applicato la seguente formula:
Sole al meridiano = 12h ((60-LONG) – ET)m
se il valore
((60-Long)-ET) è minore di zero occorre porre l'ora a 11 e sottrarre i minuti a
60.
Con LONG uguale al
valore della longitudine del luogo espressa in minuti, e con ET l’Equazione del Tempo
(in Tabella 1 sono riportate sia l’E.T. che la
declinazione del Sole per particolari periodi dell’anno).
Per esempio, volendo stabilire l’orario del transito del Sole al meridiano passante per Firenze, il giorno 1 del mese di ottobre abbiamo:
Longitudine
di Firenze (in minuti) = 45.03
E.T. del 1° ottobre = 11.2m
Sole al meridiano alle 12h (14.97 – 11.2)m = 12h 3m 46s circa.
A questo punto occorre segnare il punto su cui l’estremità del chiodo ha proiettato l’ombra, e prendere nota dell’esatta lunghezza del chiodo dalla base della tavola (AB) e della distanza, che separa il punto così trovato, dalla normale passante per la base del chiodo (AC).
L’angolo (i), la cui tangente è AC/AB, indica la declinazione del muro (maggiore di 0 se l’ombra viene proiettata a destra del chiodo – declinante a est; minore di 0 se proiettata a sinistra – declinante ad ovest).
Il compito umano è così concluso: adesso non dobbiamo far altro che dare delle informazioni al computer ed attendere che venga completata la procedura di calcolo; infatti, una volta mandato in esecuzione il programma, è necessario inserire, negli opportuni campi, alcuni dati: la dimensione della base della meridiana, l’inclinazione della parete e la latitudine geografica del luogo in cui si trova il muro. In base alla dimensione del lato orizzontale della meridiana, il programma calcolerà automaticamente la lunghezza dello stilo. In ogni caso è sempre possibile modificare una delle due grandezze (o entrambe) sino ad ottenere le dimensioni ottimali confacenti alle nostre necessità.
Prima di illustrare nei dettagli i valori numerici che il programma riporterà come risultato dei calcoli (che ci permetteranno di costruire fisicamente la meridiana), occorre tenere in considerazione alcune cose.
L’apice della
meridiana (C1) coincide sempre con il punto mediano del lato superiore della meridiana
(Fig.2).
Tutti gli angoli riportati nelle formule seguenti devono espressi in radianti: la trasformazione gradi->radianti si effettua semplicemente dividendo per 57.29577951 il valore espresso in gradi.
I valori ottenuti tramite le funzioni arcsin, arccos e arctan devono essere moltiplicati per 57.29577951 per essere espressi in gradi.
Il valore pgreco si ottiene da 180/57.29577951.
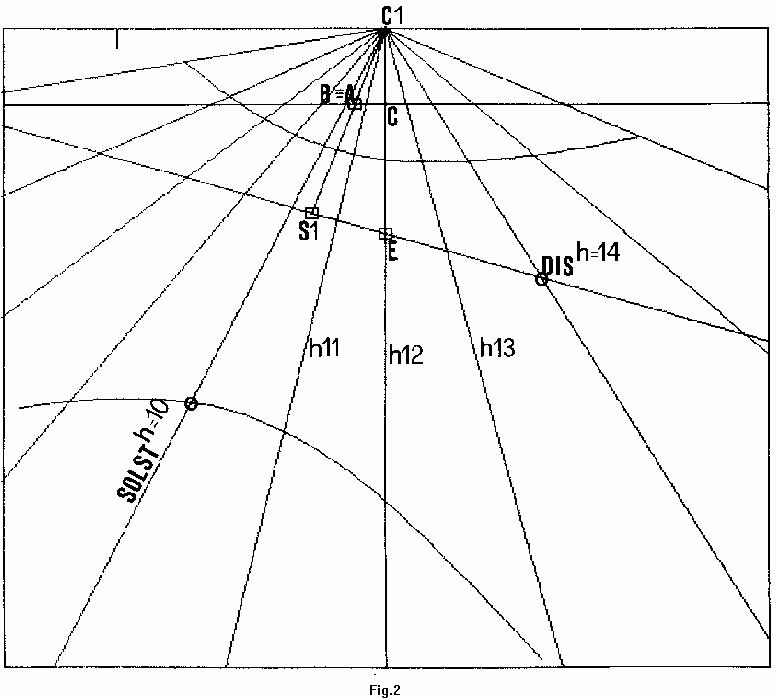
La prima lunghezza a venire calcolata è quella relativa al segmento C1 C con
C1 C = AB * Tan (LAT) / Cos(i)
e poi, per tracciare la linea equinoziale, cioè la retta su cui l’ombra dell’estremità dello stilo verrà proiettata quando il Sole sarà agli equinozi – quindi con declinazione 0 gradi – occorre fissare sia il punto (E) sulla verticale (cioè sulla linea delle 12) con
C1 E = AB * (Tan (LAT) + Tan (pgreco/2 – LAT)) / Cos(i)
sia il punto (S1) (piede del segmento che, partendo dall’apice C1, è normale alla linea equinoziale, e passa per il punto (B) su cui è posizionato lo stilo – in pratica la sottostilare) con
C1 S1 = C1E * Cos(ANG)
dove ANG è l’angolo sotteso dalla verticale e dalla sottostilare, ed è dato dall’arco la cui tangente è
Sin(i) / Tan(LAT)
E’ così determinata la linea equinoziale S1 E.
Per tracciare le linee orarie, partenti tutte dall’apice C1, non si fa altro che determinare l’intercetta di tali semirette con la linea equinoziale infatti, dopo aver determinato gli angoli (U) e (P) ed il segmento (R) con
U =
ArcCos(Sin(LAT) / Cos(ANG)
P = ArcSin(Sin(ANG) / Cos(LAT)
R = C1S1 * Sin(U)
si possono facilmente trovare tutti i punti d'intersezione (nel tabulato dei dati si hanno i valori che permetterebbero di tracciare le linee orarie ogni 6 minuti – per non rendere confusionaria la meridiana si consiglia di tracciare le linee delle ore e, al massimo, quelle delle mezz’ora) con
DISh = R * Tan(P – AO)
dove DISh rappresenta la distanza (col segno – se il punto cade a sinistra della sottostilare, col segno + se cade a destra – viceversa se la latitudine del luogo è inferiore a 0) dal punto S1 del punto d’incontro delle linee orarie (h) con la linea equinoziale, e AO l’Angolo Orario del Sole (dalle 6 A.M. alle 18 P.M., cioè da +90° a –90°, ad intervalli di 15° equivalenti ognuno ad un'ora).
A questo punto, utilizzando i dati relativi all’E.T. ed alla declinazione del Sole in epoche particolari (vd. Tab.1) viene calcolata l’analemna: per l’esattezza vengono calcolate le coordinate di 44 punti, tutti nelle immediate vicinanze della linea prescelta (in questo caso quella delle 12) che poi vengono collegati tra loro. Inoltre vengono tracciati, sull’analemna stessa, dei trattini indicanti l’inizio dei 12 mesi dell’anno ed il relativo numero d’ordine.
Successivamente vengono tracciate le linee solstiziali, sempre sfruttando sia i dati relativi alla declinazione del Sole il 21 giugno ed il 21 dicembre, che i vari angoli orari dello stesso nei vari momenti della giornata. SOLSTh indica la distanza dall’apice (C1), sulle varie linee orarie (h), che fissa il punto in cui l’estremità dello stilo proietta l’ombra nelle suddette epoche solstiziali; infatti, trovato il segmento B C1 con
![]()
e gli angoli D con
D = ArcTan(1 / ((1 / Tan(U)) * Cos (P – AO)))
si passa al calcolo di SOLSTh con
SOLSTh = BC1 * Cos(DECL) / Cos(DECL + D)
A questo punto tutti gli elementi che compongono la meridiana sono stati messi in grafica e non resta altro che passare alla costruzione pratica della stessa.
Il tabulato dei dati riporta le distanze e gli angoli che bisogna rispettare per poter tracciare correttamente tutte le linee; inoltre vengono indicate quelle misure relative a linee orarie ed a rami d’iperbole che riguardano momenti differenti da quelli basilari, come le linee ogni 6 minuti o le linee che, tra il solstizio di primavera e quello d’inverno, contraddistinguono i punti su cui l’estremità dello stilo proietterà l’ombra in relazione alla declinazione che il Sole assumerà nei vari periodi dell’anno.
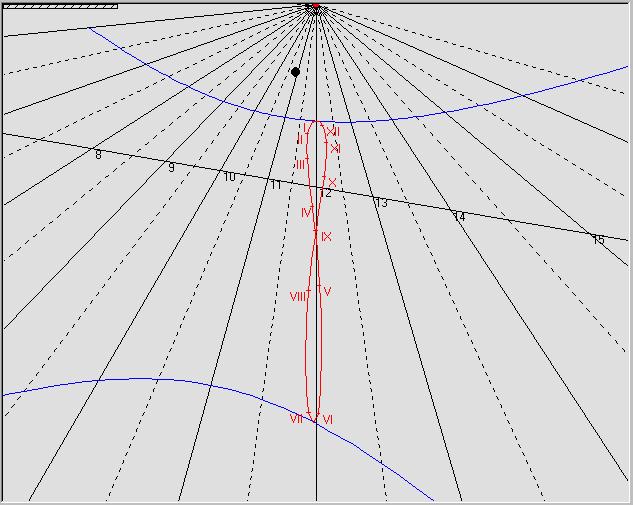
In fig.3 possiamo vedere la rappresentazione grafica dei suddetti calcoli relativi ad una meridiana solare costruita per una latitudine di 37.5N, con linee orarie calcolate ogni mezz'ora ed applicabile su una parete declinante ad est di 10 gradi. Sullo stesso grafico, nella parte in alto a sinistra, è riportato lo stilo nella sua lunghezza.
Occorre tenere in considerazione due cose:
1) il grafico ottenuto dal programma è solo approssimativo e serve solo per
dare un'idea di ciò che si otterrà (i rapporti tra le distanze non sono
rispettati);
2) è possibile posizionare lo stilo, anziché in verticale nel punto A (come
previsto dalle istruzioni sopra riportate), inclinato in modo che tutta
la sua ombra si potrà stendere sulla linea oraria. Nel primo caso l'ora verrebbe
indicata dal punto sommitale dell'ombra dello stilo, nel secondo caso, se la
meridiana è ben costruita, l'ombra seguirà gran parte della linea oraria che rappresenta l'ora in questione.
Dove e come posizionarlo?
La base dello stilo si posiziona sul punto C1 e la sua estremità
dovrà essere posizionata sulla verticale al punto A. Ovviamente a questo
punto la sua lunghezza dovrà essere ridimensionata, ma è facile ricalcolarla
poichè la distanza che separa la sua estremità superiore dalla base
(punto A) dovrà essere uguale a quella precedentemente calcolata (AB).
La base del triangolo rettangolo A-B-C1 c'è già ed è A-C1.
La nuova lunghezza sarà RadiceQuadrata(AB^2 + AC1^2).